 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |


 La
espiral equiangular o logarítmica.
La
espiral equiangular o logarítmica.
Introducción
Su ecuación es de la forma
Una primera diferencia con respecto a las espirales arquimedeanas que salta a la vista es, que el radio de posición en un punto NO DEPENDE de forma potencial (es decir, en alguna potencia) del ángulo girado, pues su dependencia es de forma exponencial.
Si despejamos de esta ecuación el ángulo en función del radio, obtenemos la ecuación:

donde vemos que el ángulo es proporcional al logaritmo del radio.
Matemáticamente, se incluye en la categoría de curvas mecánicas, es decir aquellas cuya ecuación no es un polinomio.
Su historia:
El origen del estudio de esta espiral tiene que ver con la navegación. En los siglos XVI y XVII miles de barcos surcan los océanos. Los navegantes sabían que sobre la superficie terrestre la distancia más corta entre dos puntos es un arco de círculo máximo. Pero para seguir un rumbo que encaje con este arco es necesario realizar continuos cambios de dirección. Por ello sustituían este rumbo óptimo por otro en el ángulo que formaba la trayectoria del barco con todos los meridianos que atravesaba se mantenía constante (i.e. de dirección constante). Los rumbos de este tipo dibujan en la esfera terrestre una curva llamada loxodrómica. Pero los navegantes no trabajaban sobre una esfera, sus mapas eran planos, proyecciones de la esfera. Pues bien, la proyección de la esfera sobre un plano convierte a la loxodrómica en una espiral equiangular.
Fue descrita, por primera vez, por René Descartes(1596-1648), quien un año después de la publicación de "La Géométrie", se va encontrar con la curva mecánica que responde al problema planteado por Galileo sobre la trayectoria de la caída de un cuerpo atraído por la tierra en rotación. Esta trayectoria llevó a Descartes hasta la espiral equiangular o logarítmica quien en 1638 comunicó a Mersenne sus investigaciones sobre esta curva.
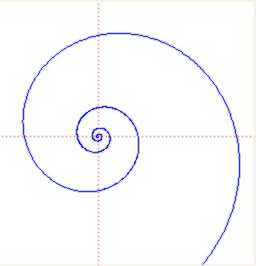
Descartes también demostró que esta condición es equivalente al hecho de que el ángulos de giro es proporcional al logaritmo del radio vector. De ahí su segundo nombre de espiral logarítmica.
Si cualquier parte de la curva es escalada para arriba o abajo, llega a ser congruente a otras partes de la curva. Las longitudes de los segmentos de la curva (líneas rojas) cortados por los radios igualmente espaciados (líneas verdes) forman una secuencia geométrica, al igual que los segmentos de cualquier vector del radio cortado por la curva que también son una secuencia geométrica. En la figura, los puntos son puntos en un espiral equiangular de 85 grados.
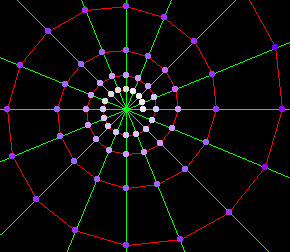
De aquí su tercer nombre de espiral geométrica.
Pero, sin duda, al matemático que más le cautivó el estudio de esta espiral fue a Jacob Bernouilli (1654-1705) , a quien le debemos el nombre de espiral logarítmica y quien la bautizó con el nombre de Spira Mirabilis, espiral maravillosa, título de su obra dedicada a esta espiral. Tanto le encantó que dejó escrito en su testamento que, en su lápida debería figurar una espiral logarítmica con la inscripción:
"Eadem mutata
resurgo" - Resurjo cambiada pero igual -.
En el cementerio de matemáticos de Basilea se puede apreciar su lápida con una espiral, que por ironía de la historia, y por ignorancia del cantero que la realizó, resulta ser una espiral arquimediana.

Torricelli, utilizando métodos semejantes a Arquímedes, fue quien primero logró calcular la longitud de la curva.
Con la aparición y el desarrollo del cálculo diferencial e integral de Newton y Leibniz, el estudio de las curvas alcanza su momento de gloria. Dentro de estas curvas no podía faltar nuestra espiral equiangular, logarítmica o geométrica.
Aunque Descartes y Torricelli habían iniciado su estudio, les faltaba la potente herramienta del cálculo para poder rematarlo. Este honor lo tomó Jacob Bernouilli en los albores del siglo XVIII.
Se construye trazando sucesivos triángulos rectángulos semejantes, de tal forma que la hipotenusa de uno es un cateto del siguiente y seguidamente se unen los vértices consecutivos.
Esta construcción se basa en la siguiente propiedad descubierta por Bernuilli:
"Mientras
el ángulo de
giro crece en progresión aritmética, el radio
correspondiente crece en progresión
geométrica"
Jacob Bernouilli descubrió varias propiedades de esta curva que les pasaron desapercibidas a Descartes y Torricelli, entre ellas el hecho de que la espiral logarítmica es la única curva que verifica que su evoluta, su involuta, su caústica, su podaria, etc., son, a su vez, una espiral logarítmica.

Nos explicamos ahora el "Eadem mutata resurgo" atribuido por el bueno de Jacob Bernouilli a esta espiral: aunque me cambien, es decir si trazan mi evoluta, mi involuta, mi caústica de reflexión o de refracción... siempre volveré a aparecer semejante a mí misma.
Jacob Bernouilli había descubierto además esta otra extraña propiedad, la autosemejanza, que relaciona directamente esta espiral con los objetos fractales.

La figura anterior muestra el conjunto de Mandelbrot, uno de los objetos fractales más populares. Investigar el sinfin de formas y estructuras que contiene sería un trabajo complejo. Sin embargo, si en este conjunto se realizan sucesivas ampliaciones sobre una de sus partes no es díficil encontrar sugerentes estructuras de espirales logarítmicas. Se puede seguir ampliando y en todos los niveles nos volverán a sorprender. Esto no es tan extraño, la autosemejanza controla las formas fractales, lo mismo que la espiral logarítmica. La propia construcción de esta espiral nos sugiere el motivo de su abundante presencia como forma que rige el crecimiento de numerosos organismos vivos. Las dos ideas que inspiran este crecimiento son las de rotación más dilatación. Crecimiento aditivo autosemajante con enrollamiento.
Nos explicamos ahora por qué las conchas de muchos caracoles vistas frontalmente forman espirales logarítmicas: al fin y al cabo no les queda más remedio que crecer siendo siempre iguales a sí mismos.
Espiral logaritmica en la naturaleza:
Hace millones de años, antes de la aparición de los peces; en la familia de los cefalópodos, había muchas especies de animales con concha en forma de espiral logaritmica; en la actualidad hay un animal llamado Nautilus, cuya concha bisectada, podemos apreciar en la siguiente imagen:

Si observamos la concha de este nautilius es fácil comprobar que no estamos ante una espiral de Arquímedes.
¿Cuál
es la primera diferencia que
salta a la vista?
Efectivamente, según nos vamos alejando del centro, la espira se va haciendo cada vez más ancha. Y este aumento de la anchura se produce de una manera continua y uniforme.
¿Por
qué el
nautilus tiene esta extraña y elegante forma?
Si observamos la imagen del Nautilus puede apreciarse que está formada por compartimentos separados por tabiques y comunicados por un sifón. El animal ocupa el compartimentomás externo, que es de mayor tamaño. Al ir creciendo, el molusco abandona el compartimento anterior y crea uno con la misma forma pero más grande.
También hay pruebas en el arte prehistórico irlandés (unos 3000 años a.C); y si observamos las galaxias del Universo la más cercana a nosotros es nuestra vecina Andrómeda; análogamente podemos observar la forma de la espiral en las borrascas; en los efectos devastadores de un tornado y también en los pequeños tornados que se producen en los lavatorios.
Esta espiral, muy similar aunque no exactamente igual a la espiral de Durero, es la que más se prodiga en la Naturaleza, ¡gran diferencia entre un y otro tipo de espiral!
Pero es el reino vegetal el que nos muestra los ejemplos más generosos de este tipo de espirales.
Si observamos las margaritas, los girasoles, las piñas de piñones o las hojas de una rosa podemos contemplar familias enteras de espirales logarítmicas.
Haciendo click AQUI puedes construir distintos tipos de espirales Logarítmicas (cambiando los parámetros), así como su evoluta, involuta, inversa, pedal, pedal negativo, cáustica radial y cáustica paralela






